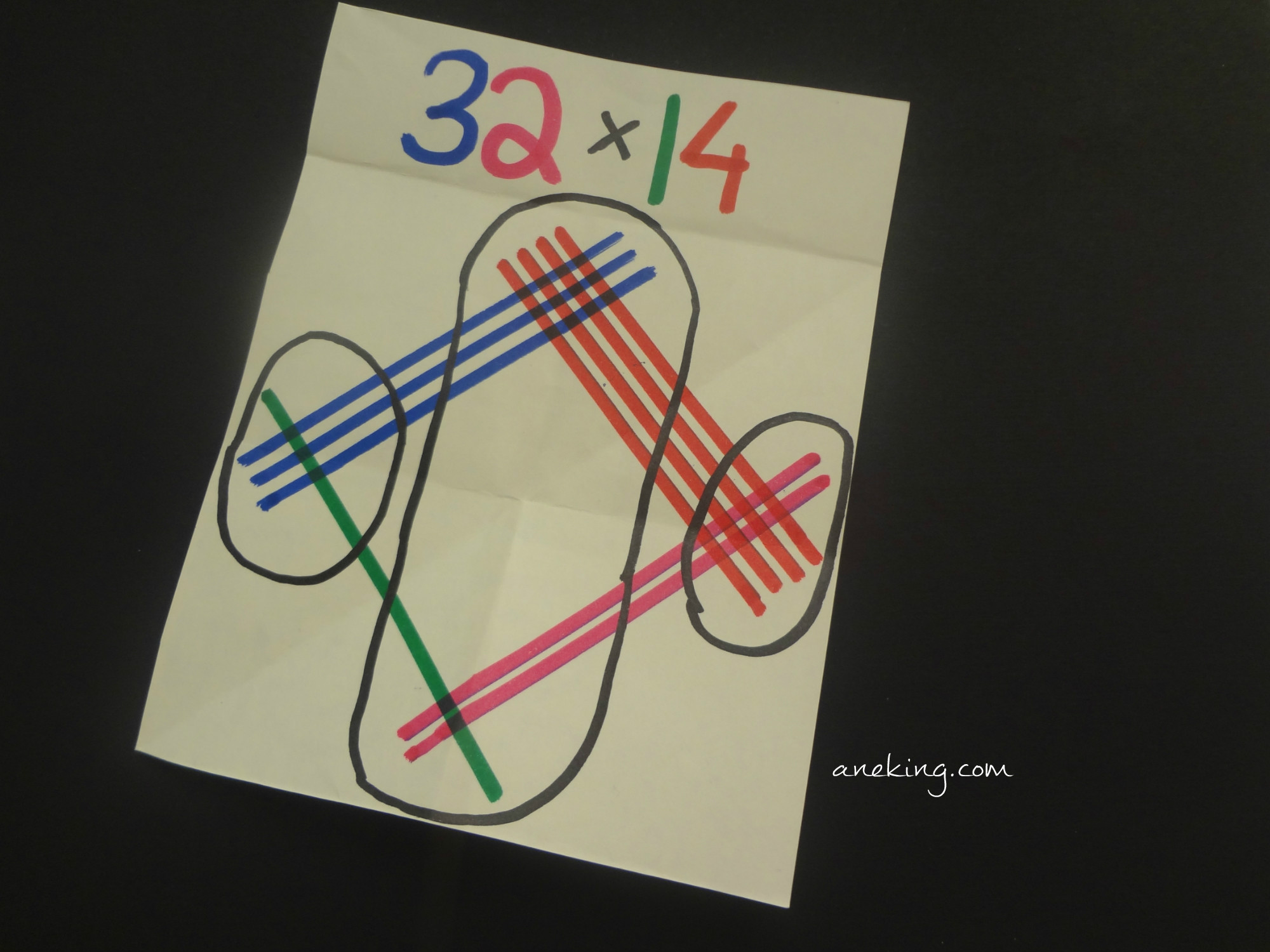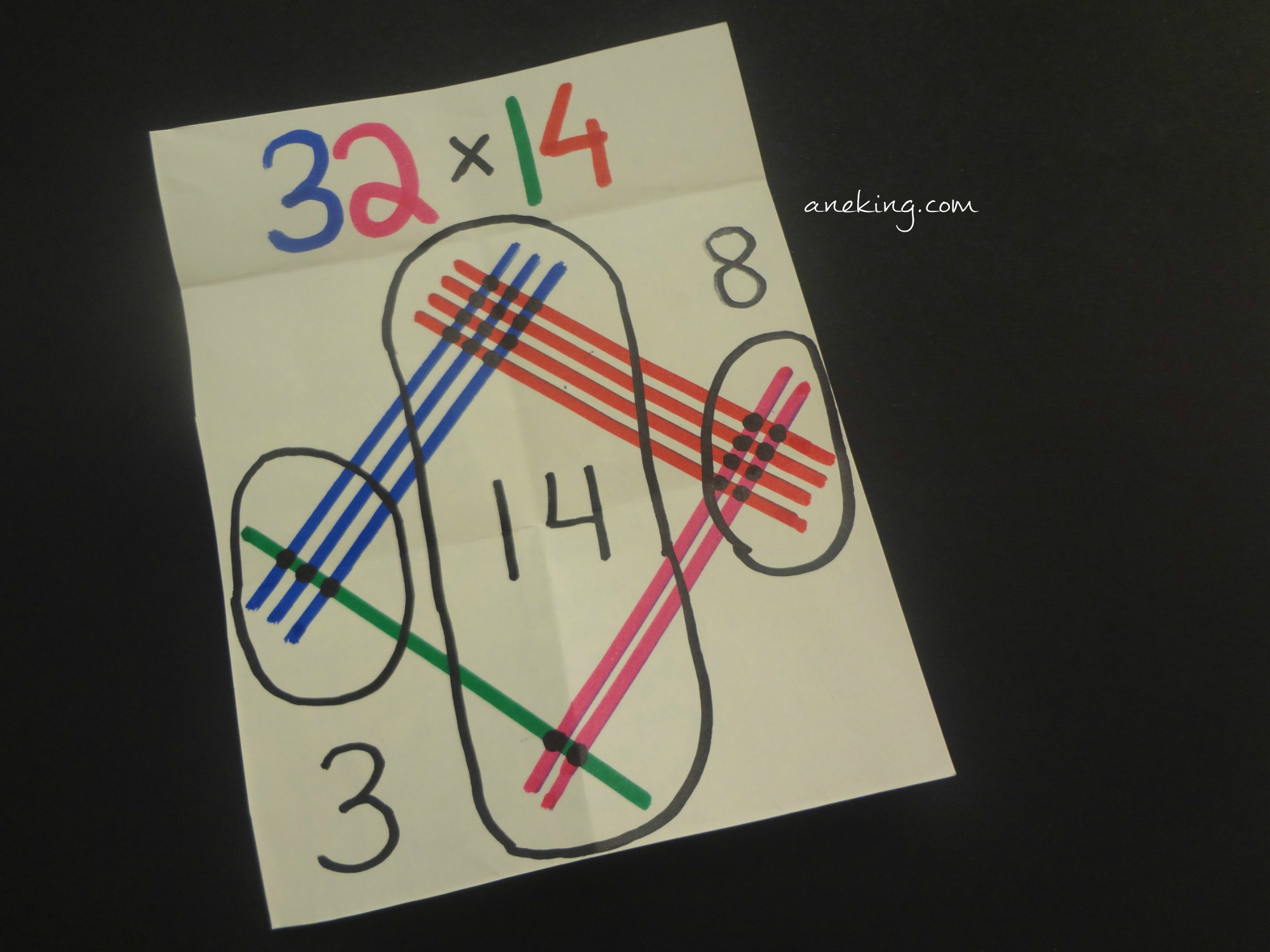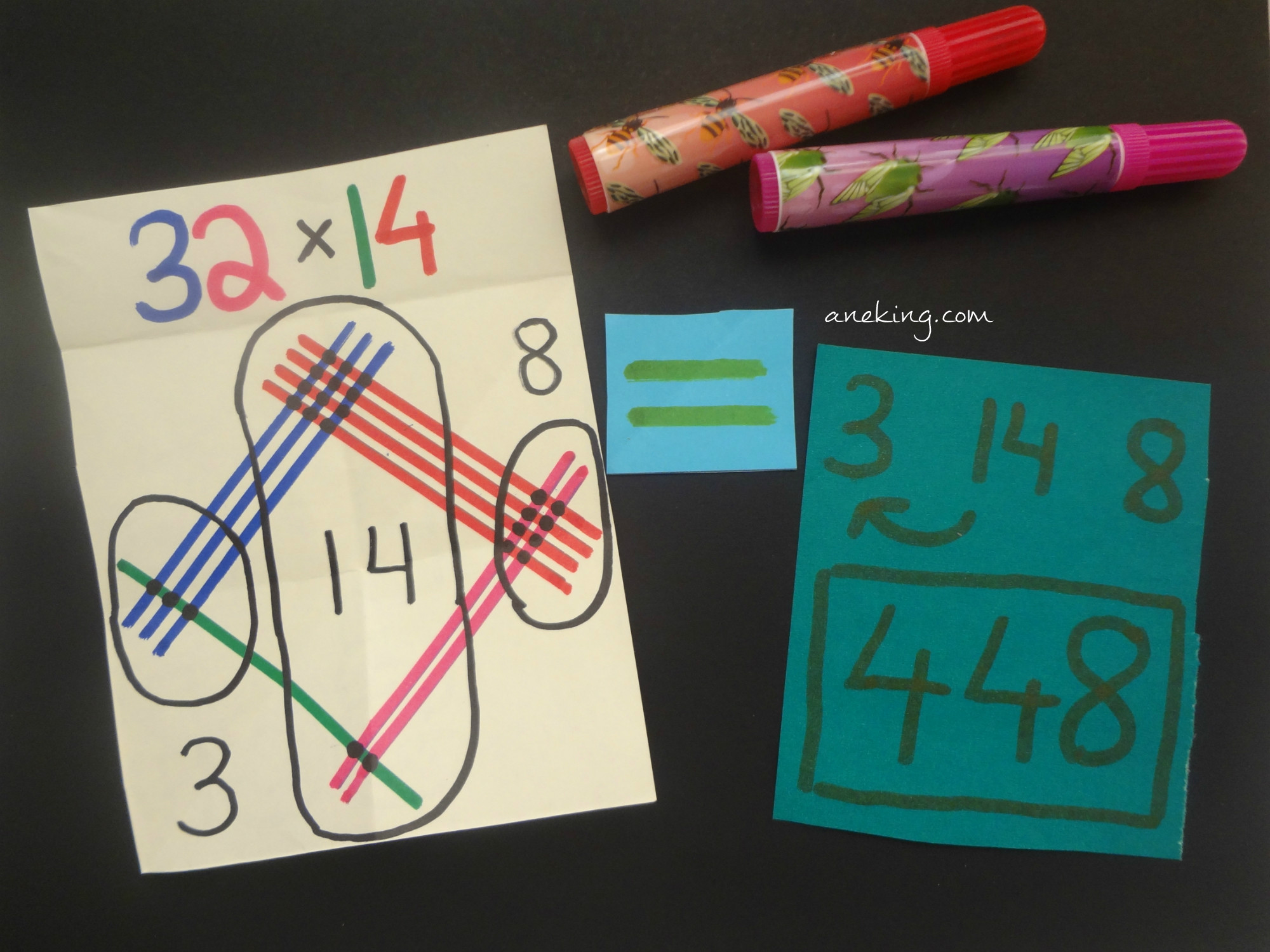How To Multiply Using The Japanese Method

Addition, subtraction, multiplication and division – we couldn’t forget these operations since this is the basics of Mathematics. In every grade and year in school, these four won’t get out of our Math lessons. Numbers may change into letters but there will always be the symbols + , – , × and ÷. We like it or not, we must like it.

But among the four, multiplication will be our topic for today. Not being proud, but I love multiplication. But for some, they find it difficult and boring. So what I’m planning to do now is to make it fun. During our grade school days, we are taught to multiply vertically and maybe, horizontally and we are forced to memorize the multiplication table. Those ways may be the most common way. Calculator is the easiest way. However, we want to know the most enjoyable way to multiply. It’s simple. Let me introduce the Japanese way of multiplying.

1. Know how to substitute numbers into lines.

2. Form these lines into grids – the tens digit of the first factor on the upper left, the ones digit of the first factor on the lower right, the tens digit of the second factor on the lower left and the ones digit of the second factor on the upper right. I used different colors for you to understand the positions better.

3. Divide this big grid into three parts. Circle the small grid on the left, small grids in the middle and the small grid on the right to separate.

4. Count the points of intersection in every circle.

5. The numbers you get are the digits of the product. The number of points on the left is the hundreds digit, the number in the middle circle is the tens digit and the number of points on the right is the ones digit. Remember that we also apply carrying into this method.